The Hadamard Matrix in Faust

17 Dec 2010

Some time ago, I had an email discussion with with Yann Orlarey from GRAME (the FAUST dsp language creator) about the best way to implement an hadamard matrix operator with FAUST. Here is a summary.

The Hadamard Matrix is commonly used in Feedback Delay Networks to maximize diffusion.

Thanks to its recursive definition:

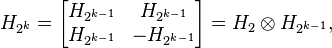
It is possible to implement it with O(n*log(N)) complexity with a butterfly structure similar to the FFT

Now how to implement this with the Faust functional dataflow language?

I. The butterfly operator

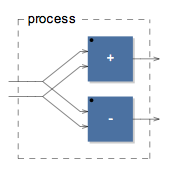
the butterfly operation for N=2 is easy:

butterfly2 = _,_ <: (+,-)

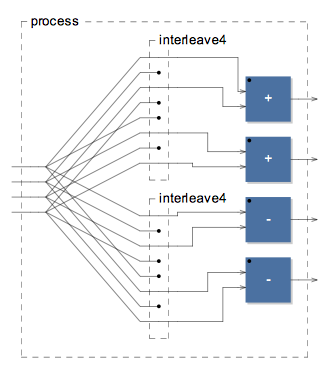
So let’s try to generalize:

interleave4 = (_,!,_,!),(!,_,!,_) ; // 0 2 1 3
butterfly4 = _,_,_,_ <: (interleave4,interleave4) : (+,+,-,-)

This one is more complicated, faust doesn’t let you explicitely make arbitrary connections between modules. We have to use the the fan out operator <: and cut unneccessary wires using operator !.  We also introduced the interleave4 helper.

So let’s try to generalize further and find a parametric version:

// selector(i,n) : select ith cable among n
selector(i,n) = par(j, n, S(i, j)) with {
    S(i,i) = _;  // pass through if i==j
    S(i,j) = !;  // cut otherwise
}; 

// interleave(m,n) : interleave m*n cables with stride m: x(0), x(m), x(1), x(1+m),...
interleave(m,n) = par(i,m*n,_)

To generalize the interleave operator we had to introduce a new helper selector that just select one cable among N. It’s quite simple to implement thanks to faust term rewriting and pattern matching rules.

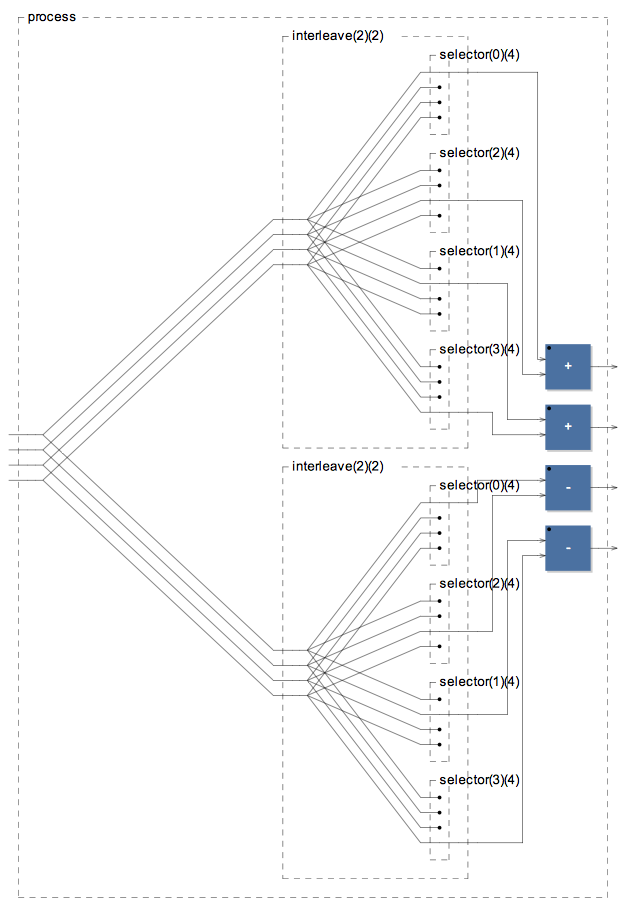
II. The hadamard matrix

Now we can easily derive the generic version of the hadamard matrix using recursion and an explicit specialization for N=2 to stop the recursion:

hada(2) = butterfly(2);
hada(n) = butterfly(n) : (hada(n/2) , hada(n/2));

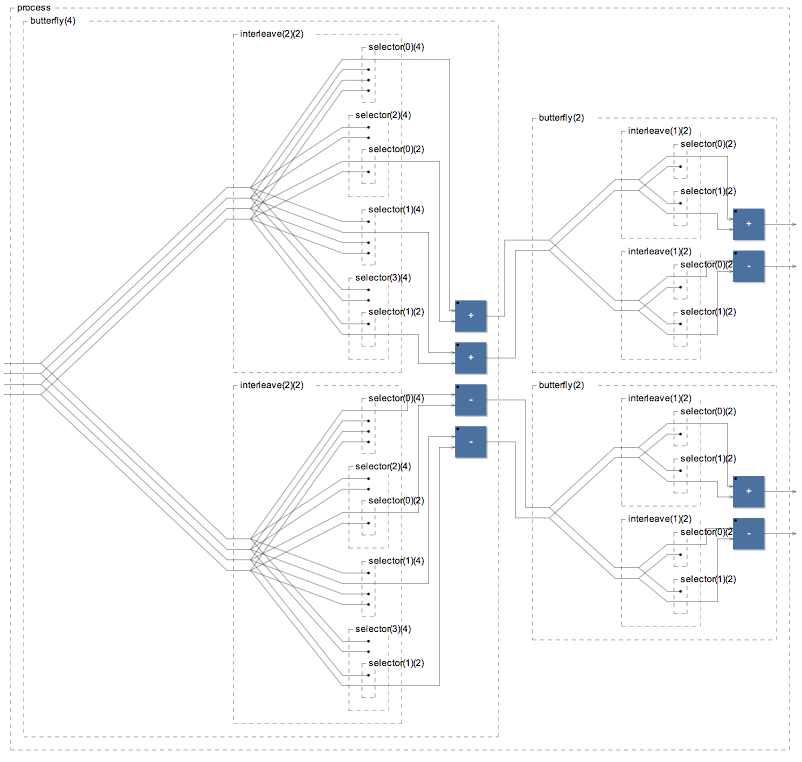
This is working correctly and we shouldn’t care much about all those wires on screen. Faust simplififes them before generating code.

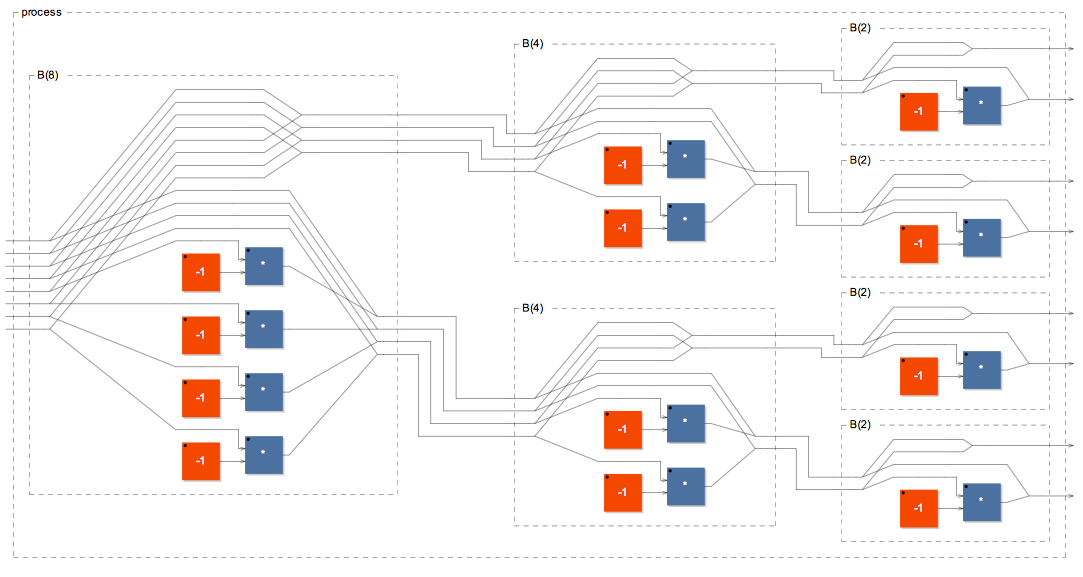
However with N=8 and above the diagram size tends to explode. Let’s try to find a more elegant solution.

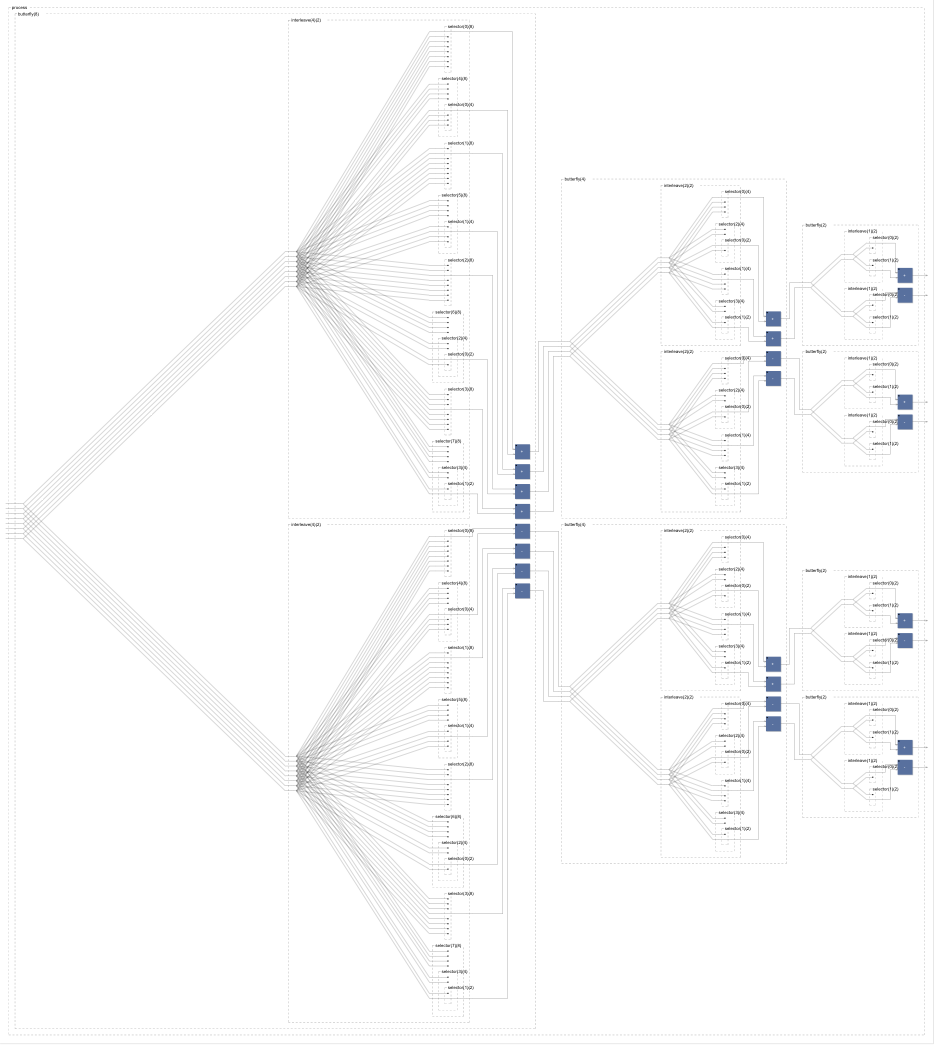
III. An alternative solution

If we look carefully at the faust merge/fanin operator :> with its implicit summation we can find a new way to write the butterfly that does almost what we need

B(n) = par(i,n,_)  par(i,n/2,_)) , (par(i,n,_) :> par(i,n/2,_)) ;

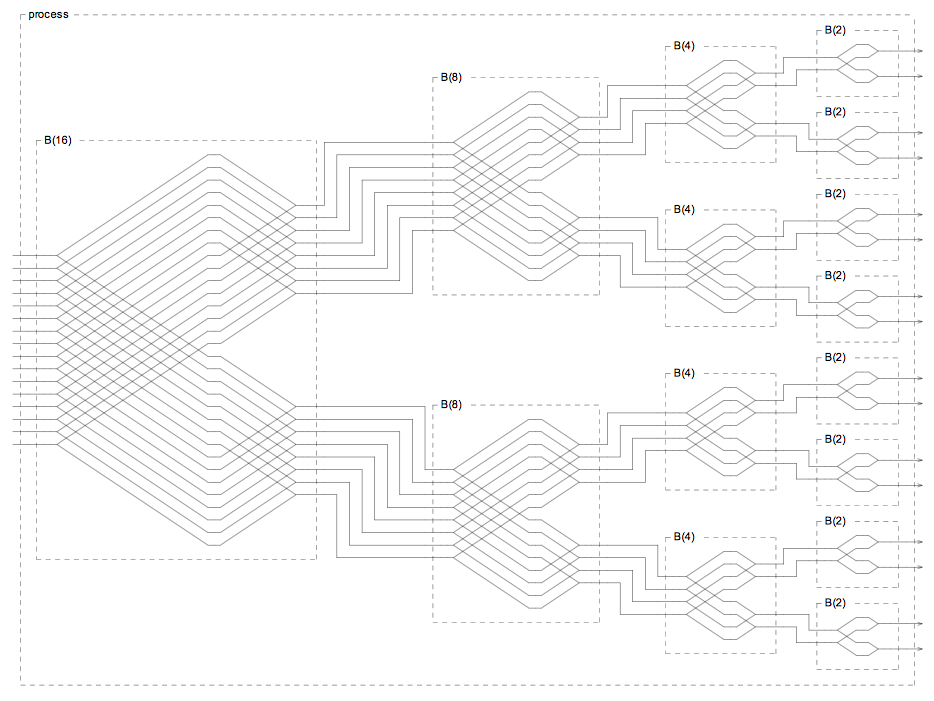
We just miss differences instead of sums for the bottom half of the graph but the display is clean compact and readable. It’s easy enough to add but unfortunately it breaks the graph symmetry and makes it harder to read.

B(n) = par(i,n,_)  par(i,n/2,_)),
                     (par(i,n/2,_),par(i,n/2,*(-1)) +> par(i,n/2,_));